回文数判断 | KMP鸿蒙算法实现

本文介绍了三种判断整数是否为回文数的算法实现。字符串法通过字符串反转直接比较，简单直观但空间效率低；数学法仅反转一半数字，时间复杂度O(log n)且空间复杂度O(1)，是最优方案；完整反转法存在溢出风险。文章详细解析了各算法的Kotlin代码实现，包括输入解析、核心逻辑和边界条件处理，并对时间复杂度进行了对比分析，推荐使用数学法作为最佳实践方案。

2501_94550878

864人浏览 · 2025-12-06 14:41:00

2501_94550878 · 2025-12-06 14:41:00 发布

在这里插入图片描述

摘要

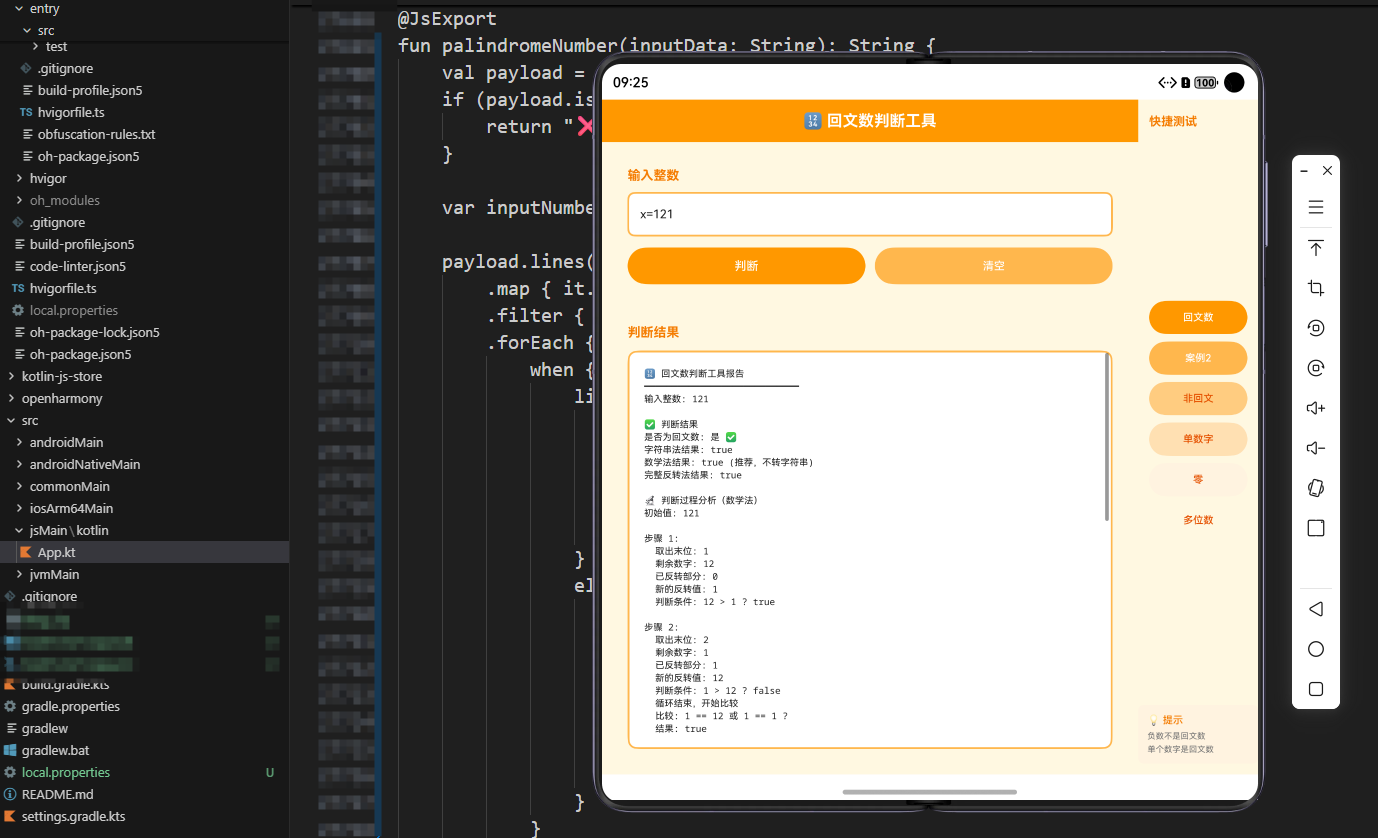
回文数判断工具实现了判断一个整数是否为回文数的功能。本文详细解析了输入解析、字符串法、数学法、完整反转法等核心功能的代码实现细节。

1. 算法背景

1.1 问题描述

判断一个整数是否为回文数。回文数是指正读和反读都相同的数字。

示例：

输入：121
输出：true（是回文数）
输入：-121
输出：false（不是回文数）
输入：10
输出：false（不是回文数）

1.2 应用场景

数字验证
密码学
数据处理
算法竞赛

2. 核心算法原理

2.1 字符串法

将整数转换为字符串，反转字符串后比较是否相等。简单直观，但需要额外空间。

2.2 数学法（推荐）

通过数学运算只反转一半数字，然后比较。时间复杂度 O(log n)，空间复杂度 O(1)。

2.3 完整反转法

完全反转数字，然后与原数字比较。可能溢出，不推荐。

3. 代码实现详细解析

3.1 输入解析模块

var inputNumber = 0

payload.lines()
    .map { it.trim() }
    .filter { it.isNotEmpty() }
    .forEach { line ->
        when {
            line.startsWith("x=", ignoreCase = true) -> {
                try {
                    inputNumber = line.substringAfter("=").trim().toInt()
                } catch (e: Exception) {
                    inputNumber = 0
                }
            }
            else -> {
                if (inputNumber == 0) {
                    try {
                        inputNumber = line.toInt()
                    } catch (e: Exception) {
                        inputNumber = 0
                    }
                }
            }
        }
    }

代码解析：

这段代码实现了灵活的输入解析机制，支持从输入字符串中提取整数。首先声明一个变量 inputNumber，初始值为 0。

然后使用函数式编程风格处理输入：payload.lines() 将输入按行分割，map { it.trim() } 去除每行的首尾空白字符，filter { it.isNotEmpty() } 过滤空行。

在 forEach 循环中，使用 when 表达式进行模式匹配。第一个分支处理 x= 格式的输入：提取等号后面的部分并转换为整数。使用 try-catch 块捕获可能的异常，如果转换失败，保持默认值 0。

第二个分支处理没有前缀的情况：如果 inputNumber 仍然为 0，则直接将当前行转换为整数。同样使用 try-catch 块处理异常。这种设计提高了输入格式的灵活性，用户可以输入 x=121 或直接输入 121。

3.2 字符串法实现

fun isPalindromeString(x: Int): Boolean {
    if (x < 0) return false
    val str = x.toString()
    return str == str.reversed()
}

代码解析：

这是字符串法的实现，通过字符串操作来判断是否为回文数。函数接受一个整数作为参数，返回布尔值表示是否为回文数。

首先检查是否为负数：如果 x < 0，直接返回 false。这是因为负数不可能是回文数（例如，-121 反转后是 121-，不是回文数）。

然后将整数转换为字符串：val str = x.toString()。这样可以将数字的每一位作为字符处理。

最后比较原字符串和反转后的字符串：return str == str.reversed()。reversed() 函数返回字符串的反转版本。如果两个字符串相等，说明是回文数，返回 true；否则返回 false。

这个方法的优点是实现简单直观，容易理解。缺点是需要额外的空间来存储字符串（空间复杂度 O(log n)），并且需要创建反转后的字符串。对于非常大的数字，这可能会消耗较多内存。

3.3 数学法实现（推荐）

fun isPalindromeMath(x: Int): Boolean {
    if (x < 0) return false
    if (x < 10) return true
    if (x % 10 == 0) return false

    var num = x
    var reversed = 0

    while (num > reversed) {
        reversed = reversed * 10 + num % 10
        num /= 10
    }

    return num == reversed || num == reversed / 10
}

代码解析：

这是数学法的实现，通过数学运算只反转一半数字来判断，这是最优的方法。函数接受一个整数作为参数，返回布尔值表示是否为回文数。

首先处理几个特殊情况。如果 x < 0（负数），直接返回 false，因为负数不可能是回文数。

如果 x < 10（单个数字），直接返回 true，因为所有单个数字（0-9）都是回文数。

如果 x % 10 == 0（以0结尾），直接返回 false，因为除了0本身，任何以0结尾的正数都不可能是回文数（例如，10 反转后是 01，即 1，不是回文数）。

然后初始化两个变量：num 是当前处理的数字，初始值为 x；reversed 是反转后的数字，初始值为 0。

接下来使用 while 循环，条件是 num > reversed。这个条件确保只反转一半数字，当反转的数字大于等于原数字时停止。这是算法的关键优化点。

在循环内部，取出 num 的末位数字（num % 10），将其添加到 reversed 的末尾：reversed = reversed * 10 + num % 10。然后将 num 除以 10（整数除法），去除末位数字：num /= 10。

例如，对于数字 121：

第一次循环：num = 121，reversed = 0
- 取出末位：121 % 10 = 1
- 更新 reversed：0 * 10 + 1 = 1
- 更新 num：121 / 10 = 12
- 判断：12 > 1，继续循环
第二次循环：num = 12，reversed = 1
- 取出末位：12 % 10 = 2
- 更新 reversed：1 * 10 + 2 = 12
- 更新 num：12 / 10 = 1
- 判断：1 > 12 为假，循环结束

循环结束后，需要比较 num 和 reversed。对于偶数位数的回文数（如 1221），循环结束后 num == reversed（num = 12，reversed = 12）。对于奇数位数的回文数（如 121），循环结束后 num == reversed / 10（num = 1，reversed = 12，reversed / 10 = 1）。

所以最终返回 num == reversed || num == reversed / 10。如果满足任一条件，说明是回文数，返回 true；否则返回 false。

这个算法的时间复杂度是 O(log n)，其中 n 是输入数字的绝对值，因为需要处理的位数是 log₁₀(n)。空间复杂度是 O(1)，因为只使用了固定数量的变量。这是最优的解决方案。

3.4 完整反转法实现

fun isPalindromeFullReverse(x: Int): Boolean {
    if (x < 0) return false
    var num = x
    var reversed = 0

    while (num > 0) {
        val digit = num % 10
        if (reversed > Int.MAX_VALUE / 10) return false
        reversed = reversed * 10 + digit
        num /= 10
    }

    return x == reversed
}