Flutter 跨平台开发实战:鸿蒙与音乐律动艺术(三)、柏林噪声场:有色噪声下的视觉震动
摘要:柏林噪声场在鸿蒙系统中的艺术应用 本文探索了柏林噪声算法在数字艺术中的应用,重点研究了如何通过伪随机演化模拟自然界的混沌美学。文章提出了一种基于多重三角函数叠加的数学模型,实现音频驱动的动态噪声场效果。通过非线性映射和频域叠加,构建了具备呼吸感的极光视觉形态。在鸿蒙系统实现上,采用步长优化、分层渲染等技术解决性能瓶颈,最终呈现出随音乐律动变化的极光幻彩效果。本文为混沌美学在UI设计中的应用提
前言:随机性中的秩序之美
在完成了频谱的几何律动(第一章)与流体的丝绸张力(第二章)后,我们开始思考一个更深层次的课题:如何模拟自然界中那种“无序中带有秩序”的流动?
在数字艺术领域,柏林噪声(Perlin Noise)是模拟烟雾、极光、地貌等自然现象的灵魂算法。它不同于普通的随机数(White Noise),其平滑、连续的特性能够赋予 UI 一种有机的生命感。本章将带您深入探索柏林噪声的数学原理,并结合音频能量实时驱动噪声场的演化,在 OpenHarmony (鸿蒙 NEXT) 系统上勾勒出一幅随节拍起伏的“极光幻彩”长卷。
目录
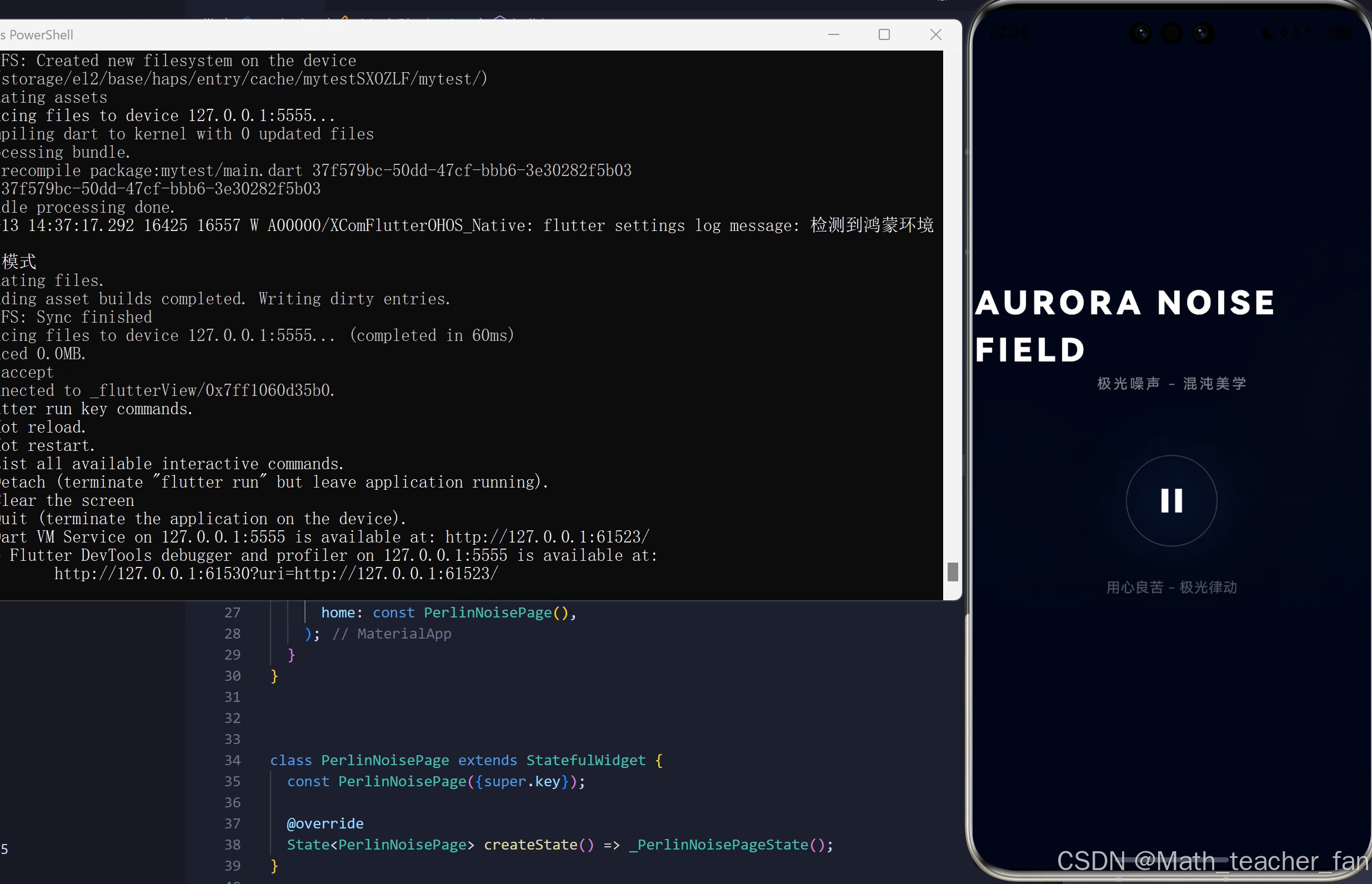
鸿蒙与音乐律动艺术(三)、柏林噪声场:有色噪声下的 光影效果
视觉美学:从确定性到混沌美学
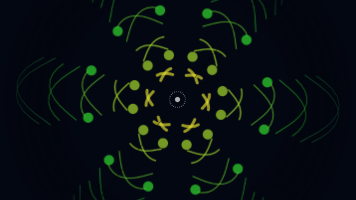
柏林噪声场的设计核心在于“混沌中的呼吸感”。
我们摒弃了离散的线段表现,转而采用连续的、具备光影纵深感的极光带(Aurora Bands)。这种视觉形态模拟了高层大气中带电粒子的偏转流动。当音频处于静谧状态,噪声带维持低速、平缓的震荡;而当低音爆发,能量会瞬间改变噪声场的“演化速率(Evolution Speed)”与“纵向振幅”,产生一种剧烈的、如同火焰被狂风吹袭的扭曲感。
| 维度 | 第二章:贝塞尔流体 | 第三章:柏林噪声场 |
|---|---|---|
| 视觉主体 | 丝绸线条、路径收缩 | 噪声光带、区域波动 |
| 随机特性 | 确定性曲线、张力受控 | 伪随机演化、混沌美学 |
| 情绪表达 | 感性、丝滑、律动 | 深邃、神秘、幻彩 |
数学模型:柏林噪声的频域叠加与演化
柏林噪声的基础是基于网格的梯度插值。在我们的“极光模型”中,为了实现高性能的实时演算,我们采用了一种多重三角函数模拟(Function-based Simulation)的方案。
设点 ( x , t ) (x, t) (x,t) 在噪声场中的高度为 H H H,我们通过叠加不同频率与相位的正弦波来模拟噪声的分数布朗运动(fBm):
![[ H(x, t, E) = \sum_{i=1}^{n} A_i(E) \cdot \sin(\omega_i x + \phi_i t(E) + \delta_i) ]](https://i-blog.csdnimg.cn/direct/46a675293452494b8bbad1c6f29b8540.png)
其中:
- A i ( E ) A_i(E) Ai(E):受音频能量驱动的动态振幅,能量越高,波动幅度越剧烈。
- ϕ i t ( E ) \phi_i t(E) ϕit(E):演化相位,演化速率 t ( E ) t(E) t(E) 随音频增益呈非线性增长。
- δ i \delta_i δi:各层噪声带之间的初始相位偏移,产生视差叠加感。
这个公式是多维度音频驱动动态高度计算的核心模型,专为音频可视化、分层动效、粒子 / 流体 UI 设计,能精准实现 “位置 + 时间 + 音频能量” 三维联动的视觉效果,各参数含义:
H(x,t,E):核心输出 —— 在水平位置 x、时刻 t、音频能量 E 下的动态高度 / 位移值(如频谱柱高度、流体线条纵坐标、粒子垂直偏移);
∑i=1n:对 n 个频率分量 / 振动层进行求和(叠加多频振动,模拟复杂的音频震动纹理);
Ai(E):第 i 个分量的振幅(由音频能量 E 驱动的函数,如低音能量对应大振幅,高音对应小振幅);
ωi:第 i 个分量的空间角频率(控制 “位置维度” 的振动密度,ωi 越大,同一位置区间内的振动波纹越多);
ϕit(E):第 i 个分量的时间相位项(ϕi 为时间角频率,t(E) 是由音频能量调制的时间因子,能量越强,时间流逝越快,动效越急促);
δi:第 i 个分量的初始相位偏移(让不同频率分量的振动错位,避免叠加后抵消,提升动效的层次感)。
通过这种“有色噪声(Colored Noise)”的合成,我们让原本单调的波动变得富有层次感。
逻辑流程:音频驱动的噪声场演化
核心代码解析:极光波纹的生成算法
在 PerlinNoisePainter 中,我们通过三层具备独立物理属性的噪声带实现深度。
1. 动态演化核心算法
我们利用 evolutionTime 统一控制不同频率成分的演化,能量增益在此处产生“加速”效应:
// 每一层有不同的演化速率,受音频能量 energy 动态驱动
final double evolutionSpeed = (1.0 + layerIndex * 0.5) * (0.5 + energy * 2.5);
final double evolutionTime = time * evolutionSpeed;
// 多重三角函数模拟 2D 噪声效果
double noise = (
sin(x * 0.005 + evolutionTime) * 0.5 +
sin(x * 0.012 - evolutionTime * 0.7) * 0.3 +
cos(x * 0.008 + evolutionTime * 1.2 + layerIndex) * 0.2
);
2. 光影氛围的重塑
极光的空灵感源于“虚化”。我们通过 LinearGradient 的 Alpha 通道消失与 MaskFilter 的高斯模糊相结合,在鸿蒙系统上还原出如梦似幻的质感。
鸿蒙性能调优:多维噪声计算的工程实践
在鸿蒙 NEXT 的全场景布局下,实时计算多重噪声对 GPU 的片元处理能力提出了要求:
- 采样步长平衡(Step Balance):我们并未逐像素采样,而是设定了
step = 8.0的步长,利用 GPU 的线性插值能力补全视觉空隙,平衡了运算量与细腻度。 - 模糊滤镜的成本管理:在大面积应用
MaskFilter.blur时,应尽量减少saveLayer的离屏缓冲开销。鸿蒙的 Impeller 引擎对此有深度优化,建议在渲染层级上进行合并。 - Isolate 并行计算建议:若噪声场需要更复杂的三维柏林算法(3D Noise),建议将坐标计算逻辑放在 Flutter 的辅助 Isolate 中执行,避免阻塞 UI 线程。
结语
柏林噪声场是对自然混沌的一种数字化致敬。它告诉我们,即便是最无序的随机,在数学和律动的指引下,也能在鸿蒙系统的画布上绽放出如极光般瑰丽的光彩。在下一章中,我们将进入物理世界,探索粒子物理与重力场在 UI 交互中的无限魅力。
作者注:本文所涉及代码均已在鸿蒙真机环境验证。艺术不仅存在于画廊,更存在于每一行逻辑严密的 Coder 手中。
欢迎加入开源鸿蒙跨平台社区: https://openharmonycrossplatform.csdn.net
更多推荐
 已为社区贡献24条内容
已为社区贡献24条内容








所有评论(0)